選択した画像 等しい 分数 の やり方 163799
等しい分数を見つける 無料で使える学習ドリル
1 自分の考えを発表する。 ①等しい分数を見つけ出し，その中から分母が等しい 分数に注目して，分子同士の比較をしたんだよ。分母 はの場合の他にもそろう場合があるよ。(40 や60) ②これま分数÷分数 の計算 分数÷分数の計算のやり方を、例題を使って確認してみましょう。 1 2 ÷ 3 5 1 2 ÷ 3 5 を計算せよ。 分数の割り算は、割る数を逆数にして掛けることで計算できます。 この操作を、
等しい 分数 の やり方
等しい 分数 の やり方-分数の比を簡単にするためには、分母を消すようにします。 つまり 分母を比べ、最小公倍数をかけることで分母を消します。 例えば、以下の比はどのようにすれば簡単になるでしょうか。 分母はそ 小5 算数 小5－34 分数の技① ・ 基本編 000 / 653 小5 算数 小5－34 分数の技① ・ 基本編 193,780 views 11K Dislike Share Save とある男が授業を
Popzgf5vqplabm
チョウ分数の解き方の手順 ①分母と分母の間に、チョウのしっぽをかく。 ②ななめにちょうの羽根をかき、分子のほうに触角をかく。 ③羽根の中に入っている分母と分子をかける。 ④分数の問題の場合、 等分というのがイメージしやすいケーキを用いると説明が分かりやすいのでおすすめです。 まずこのような例を考えてみましょう。 例題1） 2 2 個のケーキを 3 3 セット買った帯分数同士のたし算の学習プリントです。 初めから勉強する子や4年生に向けた内容なので、通分や約分はありません。 今回も前半は導入のための図をつけてあります。 意味やイメージを身につけつ
等しい分数を求める問題です。 通分と約分の導入として、しっかり学習してください。 ＊分母、分子を同じ数でかけたり、わったりして求めましょう。 等しい分数 → 通分、約分の練習① 等しい分数の意味とつくり方 ② 約分・通分の意味と約分・通分の仕方 ③ 分数のたし算とひき算の意味と計算 ④ 分数と小数の混合計算 ⑤ 時間の分数表示 ①と②については 前のページ で説明してい分数の足し算は、通分によって分母をそろえてから分子を足す ことで計算できます。 計算の手順は次の 3 ステップになります。 分数の足し算のやり方 通分（分母をそろえる） 分子同士を足す 約
等しい 分数 の やり方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
2 |  2 |  2 |
 2 | 2 |  2 |
2 |  2 | 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
2 |  2 | 2 |
 2 |  2 |  2 |
2 |  2 | 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
2 | 2 |  2 |
 2 |  2 |  2 |
 2 | 2 |  2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |  2 |
 2 | 2 |  2 |
2 |  2 |  2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 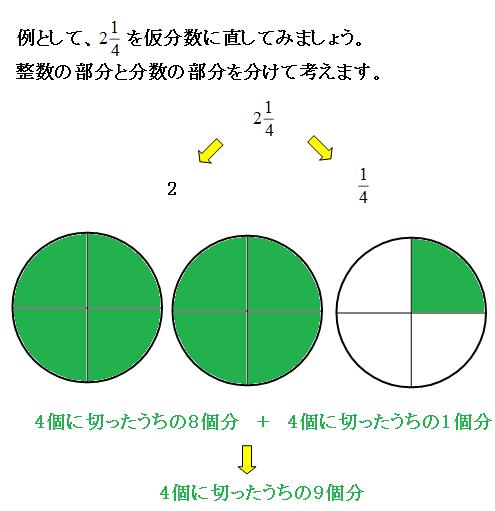 2 |  2 |
 2 |  2 |  2 |
 2 |  2 | 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |  2 |
2 | 2 |  2 |
 2 | 2 | 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
2 |  2 | 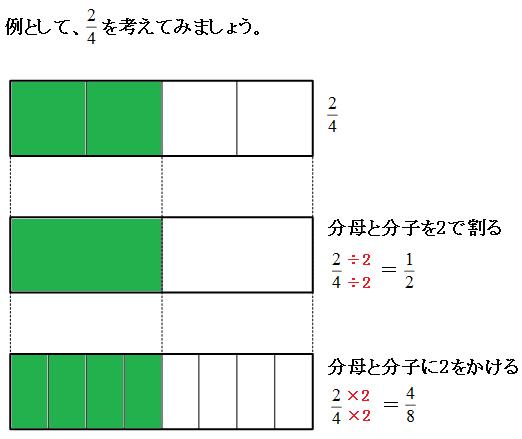 2 |
 2 | 2 | 2 |
2 |  2 |  2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
2 |  2 |  2 |
 2 |  2 |  2 |
2 | 2 | 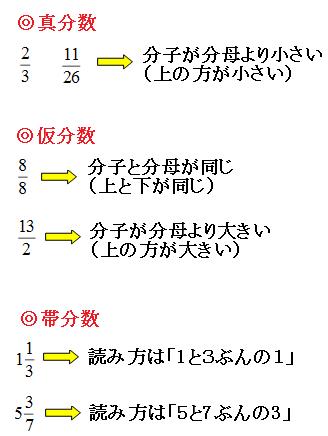 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
2 | 2 |  2 |
 2 | 2 |  2 |
 2 | 2 |  2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |  2 |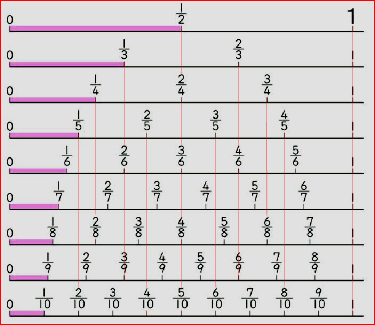
2 | 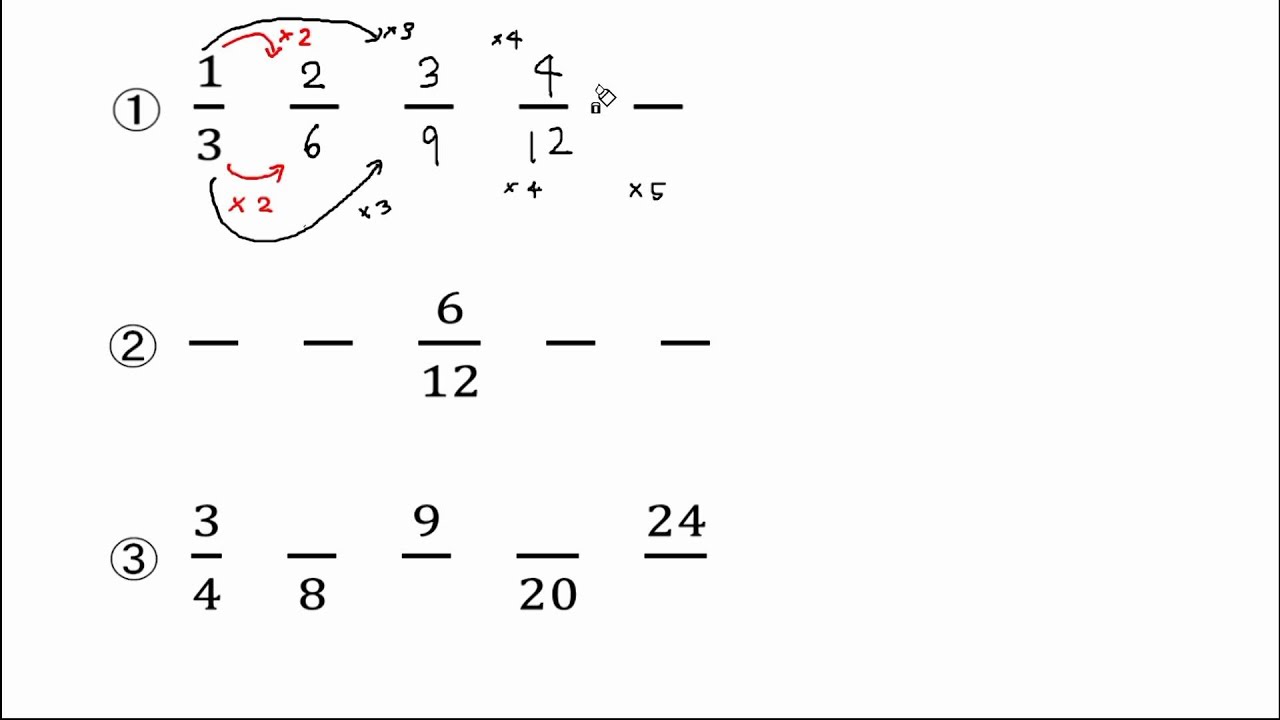 2 | 2 |
 2 |  2 | 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 2 |  2 |
2 | 2 |  2 |
 2 | 2 | 2 |
「等しい 分数 の やり方」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 2 |  2 |
 2 |  2 |
たとえば 2 2 等分したケーキ 1 1 個と 3 3 等分したケーキ 1 1 個は大きさが違うので、このままの状態ではこれらの合計を表すことができません。 そこで分母を揃える必要があり、それを 「通分」 1つのもの を、 に等しく分けた（÷ ）、〇個分（×〇）ですから、これを式に表してみると、 〇 〇 となります。 1つのものの"1"を、上の図では1つの円で考えましたが、 でも でもリボ
コメント
コメントを投稿